Page 19 - ibdaa

Ÿ-b<¡~9¡EH Ÿ-bJxƒF ˆ*]+°( * 18

—H&°* –~|ŒD*

b£K Db< I¡g~zEH $bCwD* œE b£K F]gE I¡g~zE |s~{D* “•g˜J *& œ’˜J ° ŸF&* „0° b~¦K †+ b˜ž~¦†+ ¢•< œJ]˜g†E x£= 3(* ˆ*]+°( *H
fJxƒ›D* wG h£›+ ]BH $bCwD* i*4bcg1*H ˆ*]+°( * i*4bcg1* œE h†˜/ ibFb£cD* wG *& b~¦K J&* „0°H f£<*]+°( * fBb€D* œE

f£†£c€D* f_£cD* ¤A ¤CwD* H&* ¤<*]+(°* $*2&°* ¢•< z£DH i*4bcg1°* bž›< ~{’- ¤gD* i*4]D* ¢•<

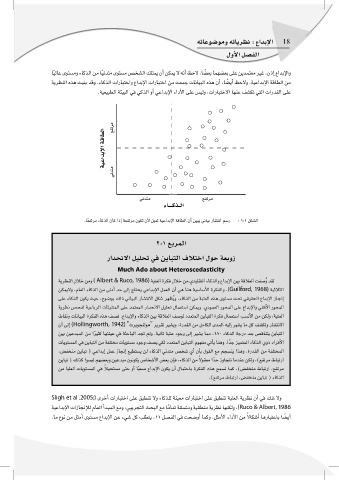
á«YGóHE’G ábÉ£dG

Êóàe ™ØJôe

Êóàe ™ØJôe

AÉ````cò``dG

b†K Œ-xE $bCwD* bC *3(* f†Œ-xE ¡’- °& –£˜- f£<*]+(°* fBb€D* *& œ£cJ ¤Fb£+ 4b~{gF* ™~64 –’~{D*

‡+x˜D*

4*]pF°* –£•p- ¤A œJbcgD* ŽÉg1* —¡0 f†+H5

Much Ado about Heteroscedasticity
fJxƒ›D* —É1 œEH ( Albert & Ruco, 1986) fcg†D* ,x’A —É1 œE ¥]£•gD* $bCwD*H ˆ*]+°( * œ£+ fBɆD* hŒ~8HO ]D
œ’˜J°H šb†D* $bCwD* œE ¢F2&* ]0 ¢D(* obgpJ ¤<*]+°( * –˜†D* &* ¤G b›G f£~6b~6°& * ,x’ŒD*H (Guilford, 1968) f£.ÉjD*
¢•< $bCwD* ¡’J k£0 r¡~9¡+ “D3 ¤Fb£cD* 4b~{gF°* –’~7 xžƒJO H $bCwD* œE fcg†D* wG I¡g~zE hp- ¤£pD* ˆ*]+(°* 5bmF(*
fJxƒF |pŒD f£<b+xD* ib_c›g˜D* ¢•< ]˜g†˜D* 4*]pF°* –£•p- —b˜†g~6* œ’˜JH ¥2¡˜†D* 4¡p˜D* ¢•< ˆ*]+°( *H ¤A&°* 4¡p˜D*
‚bFH ibFb£cD* ,x’ŒD* wG ~|- ˆ*]+°( *H $bCwD* œ£+ fBɆD* ~8¡D 2]†g˜D* œJbcgD* ,x’A —b˜†g~6* d~zF°& * œE œ’DH fcg†D*
&* ¢D(* (Hollingworth, 1942) "lxJ¡m›D¡G" xJx- x£~{JH ,4]D* œE –Eb’D* I]˜D* Ÿ£D(* x£~{J bE –C ~{’-H 4b~{gF°*
œ£+ œ£<]c˜D* œE *xK £jC bžg›£< ¤A fj0bcD* ]m- ™DH f£Fb. fcg< 2¡/H ¢D*( x£~{J b˜E $bCwD* f/42 ]†+ |Bb›gJ œJbcgD*
ibJ¡g~z˜D* ¤A œJbcgD* œE fŒ•gsE ibJ¡g~zE 2¡/H ~|J ¤’D 2]†g˜D* œJbcgD* š¡žŒE ¤-b& J b›GH *]K / y£˜g˜D* $bCwD* ¥H3 2*xA&°*
¦Œs›E œJbc- ¤<*]+*( –˜< 5bmF(* ‡£€g~zJ œD $bCwD* ¤F]gE |s~7 ¥*& &b+ —¡D* ‡E ™m~z›J *wGH ,4]D* œE fŒ•gs˜D*
œJbc- “DwC *¡~z£D ™ž~¦†+H œ£<]cE ¡F¡’J 8bs~7&°* ¦†+ b( A $bCwD* œE °K ¡†E *]K 0 5HbmgF bE]›< œ’DH ‡Œ-xE ‚bc-4*
œE b£•†D* ibJ¡g~z˜D* ¤A ÉK £pg~zE ¢g0 H*& bcK †~8 ˆ*]+°( * ¡’J &* —b˜g0b+ ,x’ŒD* wG q˜~z- b˜C ¦Œs›E ‚bc-4* ‡Œ-xE

‡Œ-xE ‚bc-4* ¦Œs›E œJbc- $bCwD*

Sligh et al Ȇ2005;) Ix1*& i*4bcg1* ¢•< c€›- °H $bCw•D f›£†E i*4bcg1* ¢•< c€›- fcg†D* fJxƒF *& ¤A “~7 °H
f£<*]+(°* i*5bmF(ÉD šb†D* *& ]c˜D* ‡EH ¤cJxmgD* kpcD* ‡E bEK b˜- f~zgEH f£€›E fJxƒF bž›’DH (Ruco & Albert, 1986
bE ˆ¡F œE –jE&* I¡g~zE ˆ*]+(°* œ< $¤~7 –C d•€gJ –~|ŒD* ¤A hp~9H&* b˜CH –jE&°* $*2&°* œE °K b’~7&* bG4bcg<b+ b~¦K J&*